A press briefing on the Australian future submarine (FSM) program by Jean-Michel Billig, the Australian program director for Naval Group (formerly DCNS), at the PACIFIC 2017 international maritime expo a few weeks ago set some hares running. Among other things, he said that ‘The vessels may end up with conventional propellers as well as air independent propulsion, which helps to increase underwater endurance’.

That was significant because DCNS made a big deal of offering Australia pump-jet propulsion during the competitive evaluation process for the FSM. We were told that ‘The Shortfin Barracuda uses a pump-jet propulsor that combines a rotor and stator within a duct to significantly reduce the level of radiated noise [compared with propellers] and avoids cavitation’. And DCNS Australia’s CEO really played up the significance of the technology:

There’s no better example of [the benefits of a strategic Australia–France relationship] than the offer from France to transfer to Australia sovereign control and use of pump-jet propulsion technology for the Shortfin Barracuda—technology resident only in France, the UK and the USA. Technology born from the French SSBN program a generation ago. The stealth and hydrodynamic performances of pump jet propulsion are of course classified and in Australia known only to DCNS and the Australian Government.

While no hard data has made its way into the public domain, an argument began doing the rounds among submarine tragics that pump jets are too inefficient at low speeds to make sense on a conventional submarine. (See here, for example, and I’ve had a stack of correspondence along those lines.) The recent Insight Economics report (PDF) has a chart (p. 103, redrawn below) that seems to show that pump jets turn electrical power into propulsion less efficiently than propellers at low speeds, though they are superior at higher speeds.

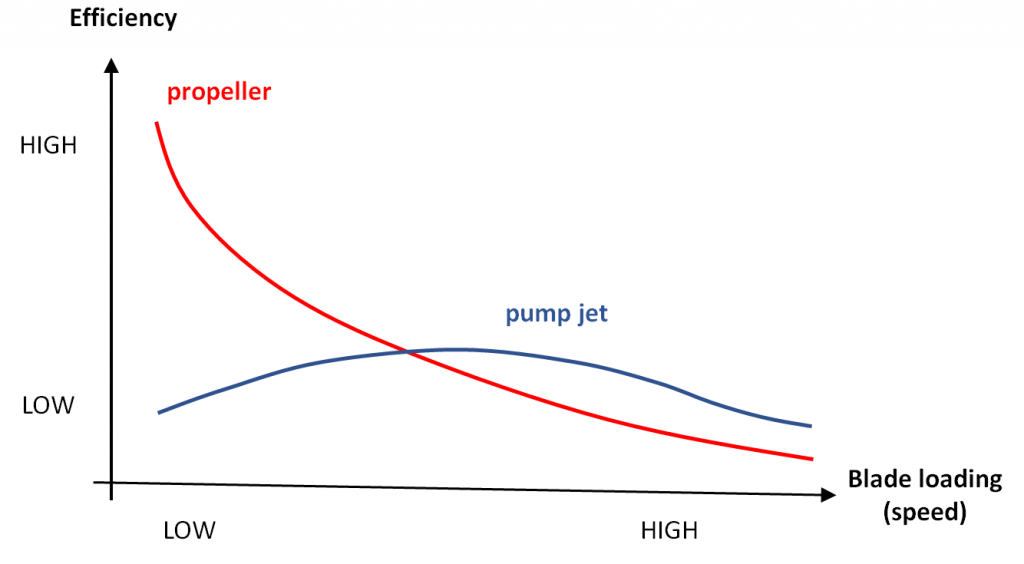
Critics of the pump jet argue that diesel-electric submarines spend much of their time at low speed, relying on batteries for power, so a propeller is the natural drive of choice for conventional submarines. That’s probably the basis for recent parliamentary questions (PDF, p. 22) about the submerged endurance of the FSM. Conversely, it’s argued, pump jets are the preferred propulsion system for nuclear submarines that travel at higher speeds and have almost unlimited power from a nuclear reactor.

I’m always wary of graphs without numbers, so I don’t know how much to read into the figure. But the argument is consistent with the observation that there are nuclear submarines around the world with pump jets (including the new French boats), but all conventionals have propellers. As I told the ABC recently, experiments with pump jets on diesel-electric boats—such as a single Russian navy Kilo-class submarine—don’t seem to have caught on. So there seems to be at least a prima facie case for propellers.

But an extraordinary claim—in this case that Naval Group is pulling the wool over the eyes of a clueless Commonwealth—requires extraordinary evidence. And on the flip side, Defence doesn’t seem to be too concerned. The department’s succinct response to a recent parliamentary question on notice was that ‘A [pump jet] can provide higher propulsive efficiency across the speed range of a submarine, including the patrol speed of conventional submarines’.

So how can we resolve the apparent discrepancy between propulsion physics (and observation of the world’s submarine fleets) and the statements of Naval Group and Defence? A possible answer is that the case against pump jets focuses on only one part of the story. If all you ever wanted a submarine to do was amble around at low speed, then you’d opt for a propeller. But there are other considerations. For a start, you want the submarine to be as quiet as possible, and the pump jet probably has the edge there. If extra stealth comes without too much performance impact, you’d take it—especially in the future anti-submarine warfare environment.

And Australia’s submarines have long transits to their patrol areas—substantially greater distances than other conventional boats—so efficient propulsion at higher transit speeds would save fuel, giving greater endurance in the patrol area. Reducing transit time is an effective force multiplier: a submarine with a 70-day endurance and a transit speed of 8 knots (representative numbers for a large diesel-electric boat like Collins) will use 31 days (44% of its total endurance) transiting to and from a patrol area 3,000 nautical miles (5,560 kilometres) from base. Reducing transit time and saving fuel potentially have a big payoff.

Another consideration is that the submarine has power requirements other than propulsion. At low speeds, the power usage can be dominated by the ‘hotel load’—the power required for onboard functions like the combat system and air conditioning. That might seem surprising, but the power required for propulsion goes as the cube of the speed—doubling the speed increases power consumption by a factor of eight. I’ve done a few simple calculations (algebra fans can see the geeky annex below), and it turns out that the submerged endurance on patrol at low speed can be many times the submerged endurance at transit speed, even if the drive is less efficient at patrol speed. I had to make a few simplifying assumptions, but a submerged endurance of over a week on batteries alone is entirely plausible, even without air-independent propulsion.

Nothing here proves that the pump-jet solution is right for the FSM, and it still might not work out. Hard numbers on noise and efficiency, including the crossover point of propeller and pump-jet efficiency, are needed for a robust assessment. It’s a safe bet that those won’t become public anytime soon, but that’s what the project office will be looking at when making engineering trade-offs during the design process.

Geeky annex

The power required for mobility at a speed is defined as , where is the power taken from the batteries and  is the efficiency of the entire drive train, including the propulsor and the main motor. If is the total power being drawn and is the hotel load (assumed constant) then . Using the cube relationship for motive power as a function of speed, a little algebra shows that the ratio of the power use at transit speed to patrol speed is:

Here is the fraction of power consumed by the hotel load in patrol conditions. To get a feel for the numbers involved, if the hotel load is 50% of the patrol power requirement, and the transit speed is four times the patrol speed, then the ratio is a little over eight, even if the propulsion is only 25% as efficient at the lower speed. That means that a day on transit power is equivalent to eight days on patrol from the point of view of total energy consumption.